海亮 DAY3 -- 字符串算法

今天计划讲解的是有关与字符串的有关算法，进行整理一下。

KMP算法

今天首先讲的算法就是KMP算法，这是有关字符串匹配有关问题的一个算法，它可以快速的计算出一个模式串在需要匹配的串中总共出现了几次，并且可以记录每次出现的位置。

其实要达到这个目的有很多办法，但是时间复杂度都比较高，差不多都是高达O(n^3)的级别的算法，而这个KMP算法则可以把时间复杂度降低到O(n+m)左右的范围。

这个算法的板子如下：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cstdlib>
using namespace std;

int nxt[1000010], now=0, ans;// 数组名字会与next冲突，所以改名为nxt或者KMP，next数组的含义是以当前坐标i为结尾的后缀s[i-j+1,i]能匹配到的最长的前缀s[1,j].
int f[1000010];// 暂时没有用
int n=0, m=0;
char a[1000010], b[1000010];

void init()//自己先匹配自己，计算出next数组。
{
	nxt[1] = 0;//因为前一位，两位失配了，都只可能将第一位作为新的开头，算是回跳的时候的一个边界条件吧
	for (int i = 2, j = 0; i <= m; ++i)
	{
		while (j && b[i] != b[j+1])	j = nxt[j];//如果失配,回跳,找到最长的前后缀重叠长度
		//此处判断j是否为0的原因在于，如果回跳到第一个字符就不 用再回跳了
		if (b[i] == b[j+1])	++j;//如果匹配成功，那么对应的模式串位置++ 
		nxt[i] = j;
	}
}

int main()
{
	cin>>a+1;//从1开始读入
	cin>>b+1;
	n=strlen(a+1);  //n a的长度
	m=strlen(b+1);  //m b的长度
	init();
	for (int i = 1, j = 0; i <= n; ++i)//i为被匹配的字符串a的指针，j为模式串的指针。
	{
		while (j > 0 && b[j+1] != a[i])	j=nxt[j];//当出现失配的情况时，直接跳到更靠前的一个位置继续开始匹配
		if (b[j+1] == a[i])	++j;//匹配成功，开始准备匹配下一个位置
		if (j == m) {
			++ans;
			//printf("%d\n", i-m+1);
			j=nxt[j];//当b串全部都被匹配的话，计数器加1，并开始下次匹配，跳到该模式串后缀匹配最多的前缀的坐标上去。
		}
	}
	printf("%d", ans);
	return 0;
}

在这个算法中，最为重要的就是Next数组了，它的含义是在模式串中以i为终点的前i个字符构成的字符串中，s[1,i]的后缀所能匹配的最长前缀的长度，即满足s[1,j] == s[i-j+1,i]。

在代码中的注释解释了KMP的主要思想。需要注意的是我们的字符串需要从1开始读入，而char的数组默认是从0开始读入，所以我们需要这样写:

cin>>a+1;

Manacher 算法

Manacher 算法是用来解决回文字符串的问题，它可以快速的求出一个字符串的最大回文子串的长度。

但是，这个算法…. 我没听懂，但是据说和KMP算法的思路很像，而且解决的问题比较单一，之后找个时间可以再看一下这个算法。
附上几个视频：

马拉车算法

一个没看懂的代码模版：

void manacher()	
{	
	int	mx=0,id=0;	
	for(int	i=0;i<n;i++)	
	{	
		if(mx>i)p[i]=min(p[2*id-i],mx-i);else	p[i]=1;	
		while(i-p[i]>=0&&str[i+p[i]]==str[i-p[i]])p[i]++;	
		if(p[i]+i>mx)mx=p[i]+i,id=i;	
	}	
}

一个巨坑，等着之后填….

Trie 树

Trie 树，又叫做字典树，应该算是一种数据结构，它可以存许多个字符串，从而可以方便的进行查询等操作。

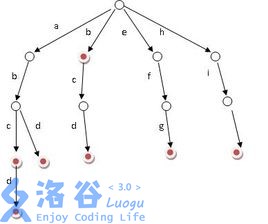
主要的原理就是一个数组模拟一个树，第一维是节点的编码，第二维是26个字母，根节点不放字符，其他的每一个子节点都可以存入一个字符，如果某一个字符串有一个节点字符，那就顺着这个节点向下，如果没有，就新建一个节点，在最后的时候用一个sum数组来储存字符串的个数，因为每个字符串的最后一个字符对应的节点编号是一定的，所以sum数组就可以确定一个字符串，而不会出现冲突等问题的存在。

模版代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int p[100010][26],tot,sum[100010],n,q,m;
char s[10010];

void insert(int now, int i)
{
	if (i > n)
	{
		++sum[now];
		return ;
	}
	if (p[now][s[i]-'a'] == 0)
		p[now][s[i]-'a']=++tot;
	insert(p[now][s[i]-'a'],)
}
int find(int now, int i)
{
	if (i > n)	return sum[now];
	if (p[now][s[i]-'a'])	find(p[now][s[i]-a],i+1);
	return 0;
}
int main()
{
	scanf("%d", &m);//  共有m个字符串需要插入
	for (int i=1;i<=m;++i)
	{
		scanf("%s", &s+1);
		n=strlen(s+1);
		insert(0,1);
	}
	scanf("%d", &q);//  共有q个询问
	for (int i=1;i<=q;++i)
	{
		scanf("%s", &s+1);
		n=strlen(s+1);
		cout<< find(0,1) <<endl;
	}
	return 0;
}

相对来说Trie树还是比较好理解的一个算法，所以没有那么多注释，理解并记住就好啦.

AC自动机

一个课件上有但是并没有讲的一个算法…具体好像就是KMP+Trie树的结合版，适用于问有几个模版串在文本串中出现过。解决多模版串的问题。

RK-Hash 算法

啊~ Hash算法，在网上看到Hash又被叫做优美的暴力，其实并不为过。字符串Hash其实就是把某个字符串与一个数字建立起联系，使之产生映射的关系。其实放在整数里的话叫做离散化，把无限空间里的量映射至有限的空间里去，这就叫做Hash。而将某一东西与数值相联系起来的函数就是h函数，它可以计算出一个东西的哈希值，并且可以肯定是唯一的值。

贴下代码，其实很简单的一个东西，但是能解决不少问题：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#define ull unsigned long long 
using namespace std;
int p[1010];
bool Hash[10000010];
char s[1010];
const ull base=131;

ull h(char s[])
{
	int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans = ans * base + (ull) (s[i] - 'a' + 1);
    return ans&0x7ffff;
}

int main()
{
	int n=0, q=0;
	scanf("%d", &n);//	一共n个字符串
	memset(Hash, false, sizeof(Hash));
	for (int i=1;i<=n;++i)
	{
		scanf("%s", &s);
		Hash[h(s)] = true;
	}
	scanf("%d", &q);//	一共q个询问
	for (int i=1;i<=q;++i)
	{
		scanf("%s", &s);
		ull t = h(s);
		if(Hash[t])
			printf("Yes\n");
		else 
			printf("No\n");
	}
	return 0;
}

对于Hash思想的应用需要不断深化理解。

有一个小的知识点，关于求一遍字符串s后，求s的字串的hash值的方法，如果每一个子串求一遍hash都需要O(n)的复杂度的话，岂不是很亏，于是我们在预处理的时候处理出一个p数组，表示在hash某个进制下某位上的权值。

于是，F区间[l,r]的hash值就可以表示为 F[r] - F[l] * 131^(r - l + 1)

小结

其实讲的还好吧，由于之前有看过有关算法，所以还算能听的懂。周围已经出现了好多全天水的人了，别放弃，坚持下去，学点东西，别让你的脑袋变成方的。今天在走廊看到一句话：当你用全部的生命去相信你能做一件事的时候，你的命运就一定会改变！加油！