海亮 DAY1 -- 搜索

发表于 | 阅读次数:
字数统计: 727 字

今天的主要内容是有关搜索的内容：

但是！

今天其实讲的很水…
有用的东西总结一下：

  1. 双向BFS搜索的代码实现

  2. 迭代加深搜索的代码实现

  3. 可行性剪枝 与 最优化剪枝

  4. 爬山算法 与 模拟退火算法(思想)

难点如下：

  1. 状态的记录
  2. 边界条件的设置

双向BFS

1
2
3
4
5
6
7
8
9
10
void	two_way_bfs()	//代码模版
{	
	while(1)	
	{
		从起点⽅向向外拓展⼀层节点;	
		if(拓展的这⼀层节点与终点拓展的节点相遇)	退出;	
		从终点⽅向向外拓展⼀层节点;	
		if(拓展的这⼀层节点与起点拓展的节点相遇)	退出;	
	}													
}

双向BFS其实就是已知初始状态与最终状态，于是就可以从头和尾同时开始BFS。当两边相遇时，退出BFS。

主要是解决最短路等问题，可以降低时间复杂度O(n的二次方) -> O(n的二分之一次方)

例题：

迷宫问题（寻找最短步数）

迭代加深搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//网上找到的一份模版，大概就是这个意思
bool dfs(int cnt, int dep) {
	if(cnt > dep) {
		if(...) return true;
		return false;
	}
	...
}
int main() {
	...
	int i;
	for(i = 1; i <= n; ++i) {
		if(dfs(cnt, i)) break;
	}
	cout<<i<<endl;
}

其实迭代加深搜索的变化就在于它限制了DFS的深度，防止出现深度过深但是正确答案不在这一棵解答树上的情况发生。

于是会有一个循环来枚举DFS的深度，防止广搜空间爆炸，DFS爆栈或超时的危险。

例题：

埃及分数（经典）

四子连棋（经典）(迭代加深60分)

爬山算法 与 模拟退火算法

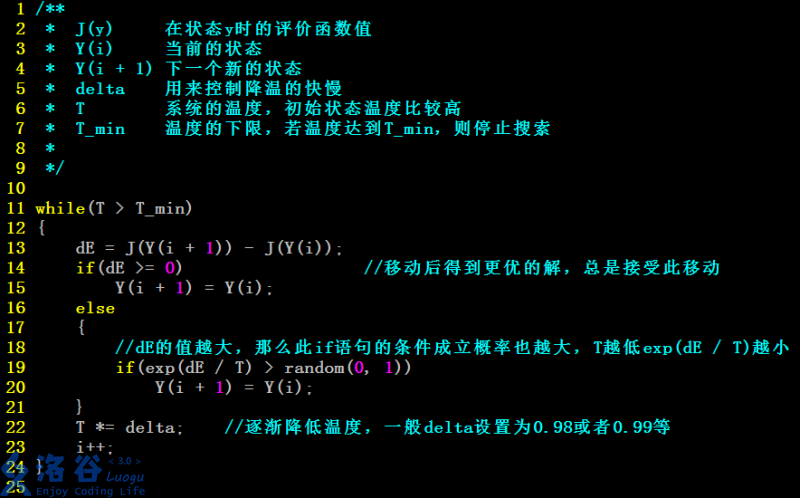
模拟退火算法的伪代码

其实模拟退火算法就是一个有点贪心的搜索，它的实现基础是基于算法的实现，不过解决了会陷入局部最优解的BUG。它在一定程度上接受了一些不是最优解的解，（这个接受是有一定的概率的！）而且接受的概率会随着时间的变化逐渐趋于一个很小的值，所以找到的解逐渐趋于稳定。

下面是爬山算法可能会遇到的问题：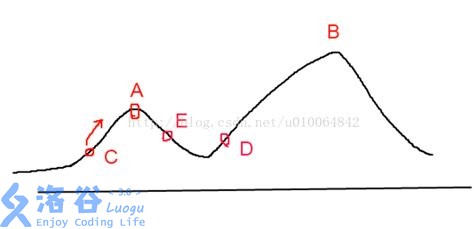
爬山算法

在这幅图中爬山算法会找到A点作为最终的答案，但是这显然是不对的，陷入了局部最优解，而模拟退火算法会避免这种情况的发生，他在开始的时候会随机的跳到一些爬山算法不会搜索到的地方，这样就解决了局部最优解的问题。

然而这对于我来说只是一个解题思路，因为这个代码实现好像很复杂的样子，具体找时间再进行代码实现。