这是一道图论题:
题面:
图G是一个无向连通图,没有自环,并且两点之间至多只有一条边。我们定义顶点v,u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点,这些顶点的集合记作I(v, u)。
我们称集合I(v, u)为一个Geodetic集合。
例如下图中,I(2, 5)={2, 3, 4, 5},I(1, 5)={1, 3, 5},I(2, 4)={2, 4}。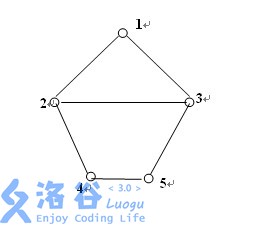
给定一个图G和若干点对v,u,请你分别求出I(v, u)。
输入格式
第一行两个整数n,m,分别表示图G的顶点数和边数(顶点编号1-n)
下接m行,每行两个整数a,b表示顶点a和b之间有一条无向边。
第m+2行有一个整数k,表示给定的点对数。
下接k行,每行两个整数v,u。
输出格式
共k行,每行对应输入文件中每一个点对v,u,按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。
样例输入
1 | 5 6 |
样例输出
1 | 2 3 4 5 |
思考
关于这道题果断floyd,因为数据大小才40,但是发现一个问题就是我不会存路径… 赶紧学了一下存路径但是才发现题目并不是在求最短路,因为这个图中可能会有很多条最短路,他要求的是所有最短路路上的点,于是我又做了了一下求所有可以使路径变短的点,可惜还不对,最后才发现只要求一边最短路,然后再枚举中间点,看是否等于最短路,并且把这个点保存下来。于是艰难AC。
代码
1 |
|