有关于数据结构的知识也接触的不少了,今天来总结一下并查集
并查集如同其名字一般,主要功能就是”并”和”查”,用来处理一些不相交集合的合并 及查询问题。
该数据结构的主要优势在于在数据量极大的情况下,能将时间复杂度保持在一个可以接受的水平之内。如果用正常的数据结构来描述的话,往往会出现空间及时间复杂度过高的情况。
由于并查集的主要操作有两种,合并和寻找,为了提高效率,我们往往在寻找的过程中使用路径压缩来保证下次查找的时候速度更快。
原理:
并查集通过一个一维数组(有些情况下会使用结构体数组)来实现。
本质上是维护一个森林。刚开始的时候,森林里的每一个结点都是一个集合(也就是只有一个结点的树),之后根据题意,逐渐将一个个集合合并(也就是合并成一棵大树)。之后寻找时不断查找父节点,当查找到父结点为本身的结点时,这个结点就是祖宗结点。合并则是寻找这两个结点的祖宗结点,如果这两个结点不相同,则将其中右边的集合作为左边集合的子集(即靠左,靠右也是同一原理)。
代码:
定义getfather函数寻找祖宗节点顺便路径压缩
1 | int f[MAXN]//用来保存每一个字节点的最高祖宗节点 |
定义merge函数,用来合并子集
1 | inline void merge(int x,int y) |
并查集的基本操作就这些,合并集合与查找,之后想起来有什么例题题解的了会继续补充
以下为几道例题:
补充:
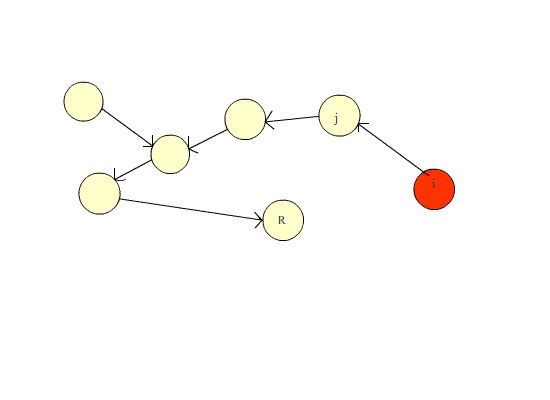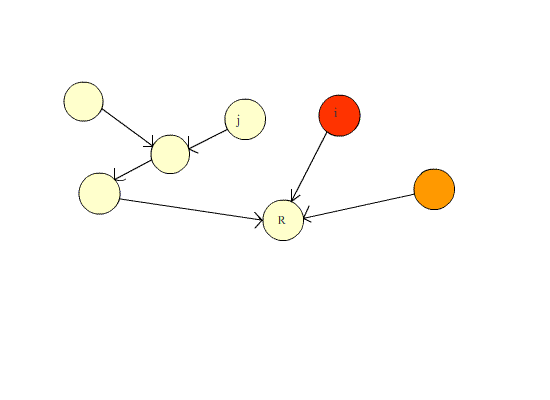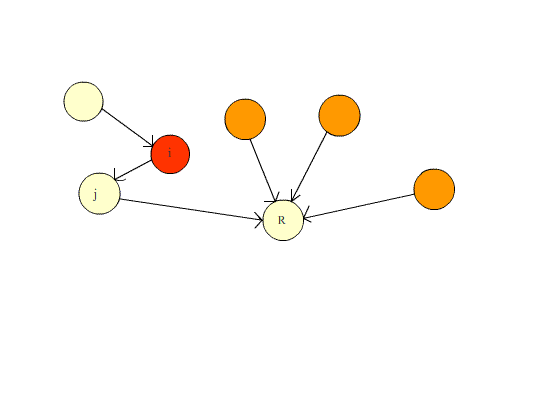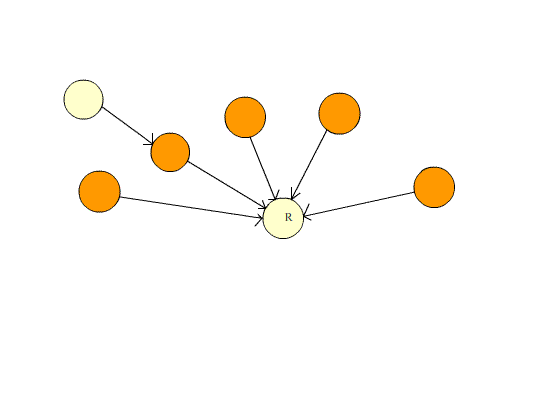
有关于路径压缩的动图演示